地政学リスクの指標 GPR-Indexの投資への応用
前回、地政学リスクGPR Indexの説明をアップロードした。
応用として地政学的影響下の石油価格(WTI)の予想値導出につながる研究結果がプレトリア大学から発表されているので、調べた内容を記録しておく。これがどれほど画期的なものかを考えるのが難しいが、GPRの真剣な応用が広がる様子が分かる。
このリンクの論文では、GPR-Indexを多変数の分散回帰に適用している(http://www.up.ac.za/media/shared/61/WP/wp_2017_02.zp106058.pdf)
研究結論としては
①VAR-BEKK-GARCHモデル という GARCHモデル(ARCHモデル - Wikipedia)の拡張版が地政学リスクこみのモデルを作る際には適当である
②石油価格と地政学リスクは関係あるが、株の平均インデックスと地政学リスクはあまり相関がない
③GPR indexのタイムラグによって石油価格と株インデックスの共分散は顕著に減少している
ここで言えそうなことはGPRインデックス算出のタイムラグを縮めると株価へ地政学リスクが波及するようになるかもしれないということである。
論文で踊っている式は、基本的にGPRに対して、価格がどれほど激しく動いているか=ボラティリティを予測する式である。ボラティリティが予測できると、ここからオプション価格をモンテカルロシュミレーションやベイズ推定などで予測できる。
導出されている式
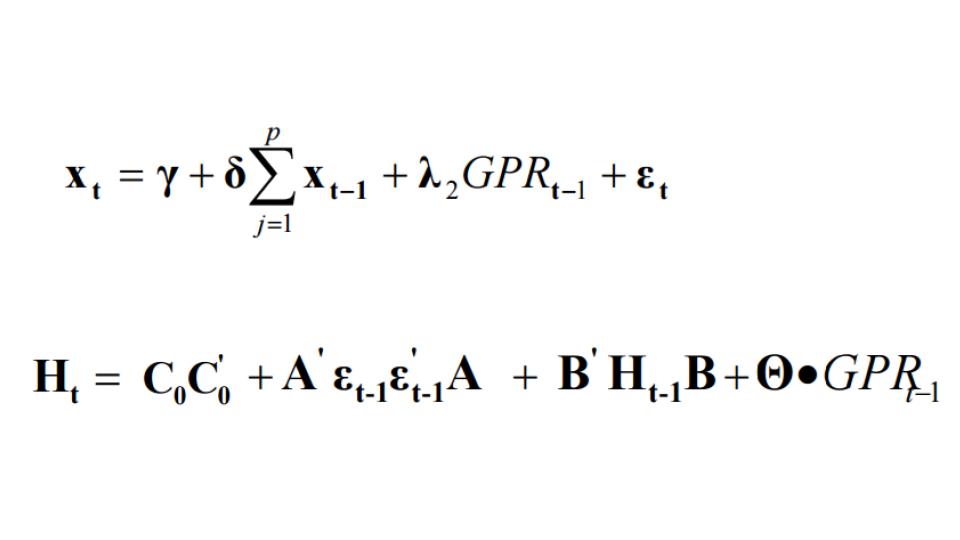
について要約を入れると
・ポートフォリオの利益 = (定数) + (ある一定期までのリターンの変動の和) + (地政学リスク×定数) + (現時点の確率変数)
・(利益の共分散) = (未知のパラメータ3つ同士の掛け算) + (未知のパラメータ4つと直前の確率変数4つ同士の掛け算) +(直前までの利益の共分散とパラメータ4つ同士の掛け算) + (係数×直前の地政学リスク)
上の式はパラメーター推定をしたあと、最終的に価格の予想につながる
下の式は、価格の予想のためのボラティリティの推定につながる。
未知のパラメーターが大量にあることに疑問を持つ方がいるかもしれない。なぜなら、このパラメータは事前に簡単に測れるものでないどころか、そもそも求まらないものだからだ。
これらのパラメータは大量の価格データと照合して、最尤法で推定されることとなる。
GPRの応用が早くもこうして十分に高度な金融工学に使われていることが分かった。次はGPRの応用が他にどのような分野に応用されるか調べたいと思う。